This time Fady decided to go for modern cryptography implementations, He is fascinated with choosing his own prime numbers, so he picked up RSA once more. Yet he was unlucky again!
Solution
We've received this two files below..
flag.b64
Ni45iH4UnXSttNuf0Oy80+G5J7tm8sBJuDNN7qfTIdEKJow4siF2cpSbP/qIWDjSi+w=
This is a base64 encoded flag message..

..decoding it returns nothing the RSA ciphered message.
key.pub
-----BEGIN PUBLIC KEY-----
ME0wDQYJKoZIhvcNAQEBBQADPAAwOQIyUqmeJJ7nzzwMv5Y6AJZhdyvJzfbh4/v8
bkSgel4PiURXqfgcOuEyrFaD01soulwyQkMCAwEAAQ==
-----END PUBLIC KEY-----
Using openssl we can get details about the Public key..
openssl rsa -pubin -in key.pub -text -noout
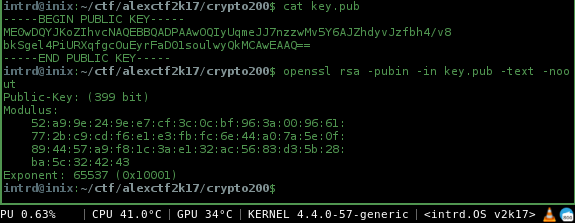
The 399 bits encryption
As you can see from public key, we have a 399 bit encryption..
In 2009, Benjamin Moody has factored an RSA-512 bit key in 73 days using only public software (GGNFS) and his desktop computer (dual-core Athlon64 at 1,900 MHz). (src: Wikipedia/RSA_(cryptosystem))
399bit is clearly insecure.
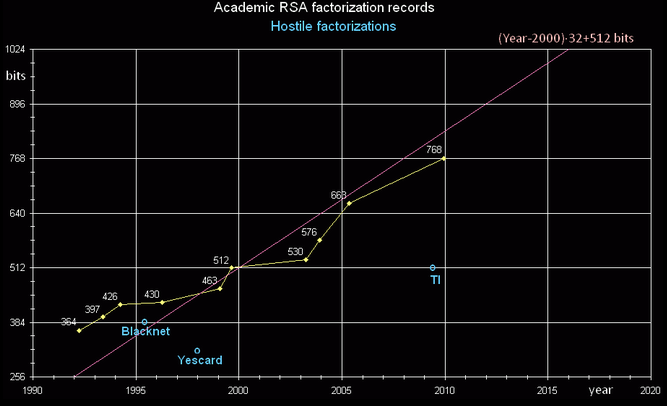 Source: https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
Source: https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
According to this evolutional graph, > 768bits is actually "secure", the minimum recommended.
Knowing this, how to decrypt our flag?
Recovering decryption key
The public key consists of the modulus n and the public (or encryption) exponent e. (Remember from the last challenge?)
- d = decryption key
To recover d we need to discover the two primes used, because the 399bit poor encryption we know this cipher used small prime numbers to generate n, so we don't need to calculate this, it can be found in factordb.com (a collective factorization data).
- n = encryption modulus (it's on the public key)
- e = public/encryption exponent (it's on the public key)
- p = first prime number (with n, factordb.com can help us to find it)
- q = second prime number (with n, factordb.com can help us to find it)
Extracting details from private key
Gmpy can automate the process to extract e and n from public key, but i'll show u how to extract manually using openssl.. It gets better to understand the big picture.
Send the pub.key content to a variable..
PUBKEY=`grep -v -- ----- key.pub | tr -d '\n'`
echo $PUBKEY | base64 -d | openssl asn1parse -inform DER -i
The modulus and public exponent are in the last BIT STRING, offset 17, so use -strparse:
echo $PUBKEY | base64 -d | openssl asn1parse -inform DER -i -strparse 17
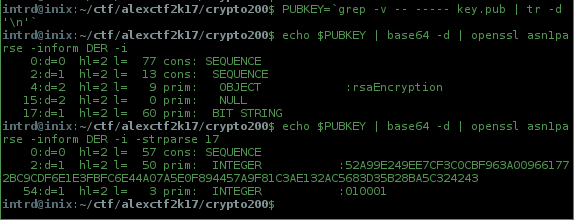
- n = 0x52a99e249ee7cf3c0cbf963a009661772bc9cdf6e1e3fbfc6e44a07a5e0f894457a9f81c3ae132ac5683d35b28ba5c324243
- e = 0x010001 (65537 integer)
Using factordb.com to get p and q
Just convert our n to integer
python -c "print(int('0x52a99e249ee7cf3c0cbf963a009661772bc9cdf6e1e3fbfc6e44a07a5e0f894457a9f81c3ae132ac5683d35b28ba5c324243', 16))"
n = 833810193564967701912362955539789451139872863794534923259743419423089229206473091408403560311191545764221310666338878019
..and do a search at factordb.com
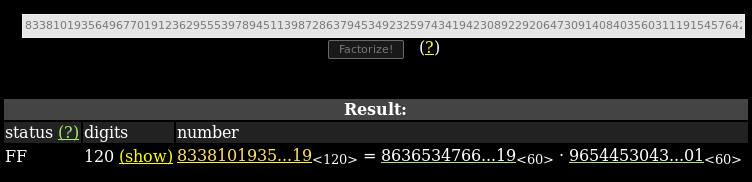
Now we have all elements to solve our problem..
- p = 863653476616376575308866344984576466644942572246900013156919
- q = 965445304326998194798282228842484732438457170595999523426901
- n = 833810193564967701912362955539789451139872863794534923259743419423089229206473091408403560311191545764221310666338878019
- e = 65537
- ct = Ni45iH4UnXSttNuf0Oy80+G5J7tm8sBJuDNN7qfTIdEKJow4siF2cpSbP/qIWDjSi+w=
To automate some things, Gmpy can help us w/ to generate the d usign p,q and e, and we do not have to worry about the conversions and the rest of boring equations.
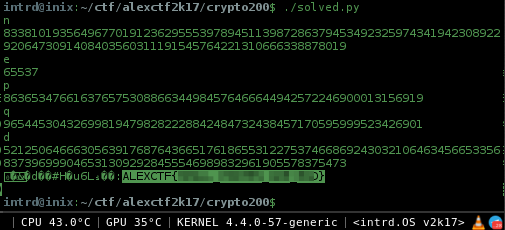
Flag: ALEXCTF{CENSORED}
 intrd has spoken
intrd has spoken